Resolución computacional de problemas térmicos y electromagnéticos en aplicaciones biomédicas

Computational resolution of thermal and electromagnetic problems in biomedical applications

Ramiro M. Irastorza[1] (UNAJ)

Resumen

En este proyecto estudiamos, mediante simulación computacional, problemas en los que se involucran múltiples fenómenos físicos de manera simultánea. De esta manera, se resuelven ecuaciones acoplando diferentes fenómenos físicos y utilizando el método de elementos finitos. En particular, nos dedicamos a la técnica conocida como ablación por radiofrecuencia (ARF), la cual se utiliza en diferentes áreas de la medicina. En esta técnica se aplica corriente de manera mínimamente invasiva en un tejido y se calienta por efecto Joule, de esta manera se busca destruir el tumor (en aplicaciones relacionadas con cáncer) o corregir arritmias (en el área de cardiología).

Palabras claves: ablación por radiofrecuencia, modelo computacional, tumor óseo, ablación cardíaca

Abstract

In this project we study by computer simulations different phenomenas in which several physics are involved. The equations are solved by coupling different physical phenomena using the finite element method. In particular, we study the technique known as radiofrequency ablation (RFA) which is used in different areas of the medicine. In this technique, a current is applied in a minimally invasive way in the tissue and it is heated by Joule effect. This tecnique can be used, for instance, to destroy tumors (in cancer- related applications) or correct arrhythmias (in the cardiology area).

Keywords: radiofrequency ablation, computer model, bone tumor, cardiac ablation

Introducción

El objetivo a largo plazo de proyecto es utilizar estas técnicas numéricas para el desarrollo de herramientas de planificación y simulación asistida por computadora para procedimientos de ablación guiados por imágenes. A mediano y corto plazo, el objetivo del proyecto es modelar experimentos in vitro en condiciones bien controladas para adquirir un mayor conocimiento de los fenómenos físicos y las propiedades térmicas de los tejidos. Se estudiaron dos casos particulares: el tratamiento de arritmias cardíacas y tumores óseos, y también problemas generales numéricos y de ablación. En este contexto nos propusimos:

• Estudiar la simulación multifísica por elementos finitos utilizando software
• Obtener un modelo de simulación numérica para la evaluación de un setup experimental utilizado para la obtención de parámetros térmicos de tejidos biológicos.
• Simular de manera realista aplicaciones de ARF (por ejemplo, con geometrías construidas a partir de imágenes de resonancia magnética).

Nuestra hipótesis es que con la simulación computacional se pueden obtener resultados similares a lo que ocurriría en la realidad. En ocasiones, en este tipo de enfoques se pueden utilizar imágenes médicas para construir modelos antropomórficos realistas de tal manera de simular la geometría lo más parecida posible al caso particular en estudio (Matschek et al., 2017).

En rasgos generales, en la técnica de ARF se coloca un electrodo activo (de pequeña superficie) en la zona a ablacionar y uno pasivo (de mayor tamaño) en otro lado del cuerpo (por ejemplo: la espalda) para cerrar el circuito eléctrico, y se hace circular una corriente de una frecuencia cercana a los 500 kHz. La ARF es utilizada para tratamiento de diferentes tipos de tumores, el más explorado es el tratamiento de hígado, aunque en la actualidad se utiliza también en riñón, pulmón, y en tejidos óseos (Brace, 2009). Otra de las aplicaciones importantes que han surgido en los últimos años es la ablación para tratamiento de arritmias cardíacas (Kobza et al., 2004). Es una técnica mínimamente invasiva y en general se aplica combinada con algún método de imágenes que permite localizar el tejido a ablacionar. La diferencia con otro tipo de tratamientos, tales como la radioterapia en cáncer, es que su aplicación es local y en una región relativamente pequeña circunscrita al electrodo de activo. En el caso de tratamiento de tumores, el acceso se hace de manera percutánea, en cambio, en el tratamiento de arritmias, una de las vías de acceso es la arteria femoral, por ejemplo.

El aumento del poder de cálculo de las computadoras y la evolución de las tecnologías asociadas al diagnóstico por imágenes ha generado un crecimiento exponencial en los estudios de modelado teórico- computacional de este tipo de problemas (Berjano, 2006). En los casos mencionados, la interacción electromagnética con los tejidos provoca un calentamiento porque pueden ser modelados como elementos resistivos, en consecuencia se debe acoplar el problema térmico (con acoplar queremos decir que ambas problemas se deben resolver simultáneamente: el térmico y el eléctrico). Las ecuaciones que rigen estos problemas se pueden resolver por el método de elementos finitos (MEF). En el trabajo de Ramiro Irastorza Irastorza et al. (2016) se estudió la ablación de un tumor óseo benigno denominado osteoma osteoide. Con estos modelos se puede estudiar, por ejemplo, el efecto aislador de la zona reactiva del tumor. En relación a otros tejidos, se pueden atacar otras problemáticas, como la evaluación del daño del tejido en la etapa posterior a la ablación (cuando se apaga la aplicación de energía). En el trabajo Irastorza et al. (2017) se compararon electrodos secos con aquellos con refrigeración interna. Este efecto es particularmente importante en el tratamiento de arritmias cardíacas (Irastorza et al., 2018), dado que en clínica se está buscando reducir el tiempo de aplicación y aumentar la potencia. Estos modelos predicen un daño posterior a la ablación que ronda el 30 % más del estimado al finalizarla.

Por otro lado, con un enfoque experimental se pueden estudiar este tipo de problemas y caracterizar las propiedades térmicas y eléctricas de los tejidos (Valvano et al., 1985; Rossmann y Haemmerich, 2014). En proyectos anteriores hemos construido y calibrado un prototipo para la medición de propiedades térmicas de tejido de manera mínimamente invasiva. Es interesante el desarrollo de este tipo de montajes experimentales porque se pueden validar los modelos computacionales (Hasgall et al., 2015).

Otro punto interesante que tratamos en este proyecto es el desarrollo de modelos realistas (Matschek et al., 2017), esto es, donde la geometría se construye a partir de imágenes de resonancia magnética o tomografía computada. Este enfoque es interesante, en primer lugar, porque nos acercamos a la geometría real y, en segundo, porque permite evaluar si los modelos de dominio limitado (de menor carga computacional) tienen la suficiente precisión.

Esta línea de investigación se encuentra en el marco del programa “Tecnologías de la información y la comunicación (TIC) en aplicaciones de interés social” de la Universidad Nacional Arturo Jauretche (UNAJ), aprobado mediante la Resolución N° 064/17, y cuyo principal objetivo es el de fortalecer la actividad de investigación dentro de la Universidad en el área de las TIC. El proyecto se desarrolló íntegramente con software libre.

Metodología

Simulaciones

En este párrafo comentaremos los resultados obtenidos mediante dos técnicas en diferentes escalas: mecánica del continuo con el método de elementos finitos (mesoescala) y modelos atomísticos con dinámica molecular (escala molecular).

Ecuaciones

Como hemos mencionado, en los últimos años, el aumento en el poder de cálculo ha generado que el modelado computacional sea una herramienta importante en particular en la ingeniería biomédica. Uno de los factores que hacen atractiva la simulación es que los experimentos y los ensayos clínicos en animales son costosos. Para la construcción de estos modelos generalmente se parte de las leyes de la física que, con habitualidad, se expresan en ecuaciones en derivadas parciales. La simulación de ARF en cualquier tejido implica dos problemas físicos acoplados y modelados por la ecuación eléctrica y la ecuación de biocalentamiento. Respecto de la primera, el calor en ARF (q_RF) es generado por el efecto Joule, aplicando una corriente eléctrica a la región deseada. Este calor depende de la conductividad eléctrica (σ) y del campo eléctrico (E) y viene dado por la ecuación q_RF = σ E ². El campo eléctrico se define como E = -∇ V , donde V es el voltaje. Este último se calcula resolviendo la denominada ecuación de Poisson en el volumen (dominio) deseado Ω:

La conductividad eléctrica puede depender de la posición y la temperatura. La Ecuación 1 es una ecuación diferencial en derivadas parciales (PDE) y se puede resolver si se conocen las condiciones de contorno. En el problema térmico, la temperatura T se obtiene resolviendo la ecuación del biocalentamiento:

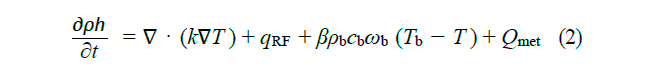donde k es la conductividad térmica, ρ es la densidad, c es el calor específico, ω es la perfusión. Q_met = 0 (calor metabólico) se establece porque es insignificante en la ARF. El parámetro β es un coeficiente que toma los valores de 0 y 1, según el valor del daño térmico (para las diferentes formas de evaluar daño térmico, ver Berjano [2006]). Los parámetros mencionados pueden ser funciones de posición y temperatura. El subíndice b indica que son parámetros sanguíneos. En cuanto al término de la izquierda de la Ecuación 2, es el término de entalpía, la idea es que capture el calor almacenado en el tejido y también los cambiosde fase que en este puedan ocurrir.

Software para MEF

El método más difundido y utilizado en la resolución numérica de estas ecuaciones es el método de ele- mentos finitos (Larson y Bengzon, 2013). Con este se pueden resolver las ecuaciones en derivadas parciales mencionadas. En general, los programas comerciales más empleados en ingeniería son: COMSOL Multiphysics y ANSYS. En nuestro caso, nos pusimos como objetivo utilizar software libre, en particular FEniCS. Este se puede usar con Python o C++, tiene mucho desarrollo actual y una muy buena documentación en línea.

Software de mallado

Para la resolución por MEF, es necesario discretizar la geometría a modelar, lo cual requiere de programas específicos. En este proyecto nuevamente se recurrió a software libre, en esta oportunidad, Gmsh, el cual permite construir geometrías relativamente simples, pero además puede importar mallas generadas con otros programas. Esto es interesante porque para la construcción de modelos realistas es importante construir modelos a partir de imágenes médicas. Para esto, utilizamos otro software libre denominado 3D Slicer. Este programa permite procesar imágenes provenientes de resonancias magnéticas y tomografías computadas (por ejemplo, en archivos dicom) y, adicionalmente, posee algunas herramientas de segmentación y filtrado que posibilita la exportación de mallas para su posterior posprocesamiento con Gmsh.

Caracterización de microestructura

También se utilizaron algunas herramientas de procesamiento de imágenes para la caracterización de microestructura de muestras óseas (como porosidad, ancho medio trabecular, dirección principal de trabéculas, etc.). En dos dimensiones, esto lo desarrollamos con Python y algunas herramientas de Scikit-image, en tres dimensiones, usamos el software ImageJ y su plugin BoneJ.

Modelos atomísticos

Como línea adicional, se comenzaron a estudiar algunos modelos atomísticos para la predicción propiedades físicas macroscópicas (propiedades dieléctricas y térmicas). Se analizó utilizando la técnica de dinámica molecular con el software GROMACS.

Experimentos

Si bien los experimentos no son la parte central de este proyecto, hemos realizado algunos para la validación del modelado en tejido óseo. Puntualmente, trabajamos en la preparación de fantomas y muestras óseas bovinas para la calibración y posterior medición de parámetros térmicos con los setups experimentales.

Preparación de muestras

Se fabricaron fantomas de agar, así como muestras de glicerol y otros para calibración de celdas experimentales. También se prepararon muestras óseas bovinas para su evaluación con microtomografía (desgrasado). Se realizó el proceso de desgrasado utilizando sonicación y detergentes específicos. Esto fue necesario para la evaluación de la influencia del contenido graso en las propiedades térmicas observadas.

Parámetros térmicos

En proyectos anteriores diseñamos, construimos, y calibramos un prototipo para la medición de propiedades térmicas de tejido, el cual utiliza un sistema de adquisición de datos (Measurement Computing MC1608GX) y electrónica desarrollada para tal fin. El setup se controla por computadora. Se realizaron experimentos con este prototipo y lo usamos para caracterizar térmicamente tejido óseo trabecular bovino in vitro y estudiar la relación con la microestructura.

Microtomografía

Con el Sistema Nacional de Microscopia, realizamos microtomografías computadas de estas muestras (Mi- crotomógrafo Bruker SkyScan 1173, gentileza de Y-TEC, Berisso, Argentina).

Resultados

En la primera etapa de este proyecto se trabajó con el estudio de la simulación utilizando software libre, dado que anteriormente se usó COMSOL Multiphysics (Irastorza et al., 2016). Algunos resultados de las si mulaciones fueron publicados durante la primera etapa de este proyecto (Irastorza et al., 2018).

Empleando el setup experimental que desarrollamos en proyectos anteriores hemos trabajado sobre la evaluación de las propiedades térmicas de tejido óseo trabecular o esponjoso (formado principalmente por dos componentes: trabéculas y médula ósea). En estos experimentos se hace un pequeño orificio en el tejido y se coloca un termistor que lo calienta localmente. Con la adquisidora se registra la etapa de calentamiento y enfriado, y con esta información se pueden obtener las propiedades térmicas efectivas del tejido (en nuestro caso, observamos difusividad y conductividad térmica). Para evaluar la propiedades térmicas de los dos componentes se generó un modelo bidimensional utilizando elementos finitos, esto luego se plasmó en una publicación (Fajardo et al., 2018). Continuamos este estudio con modelos tridimensionales construidos a partir de microtomografías (ver Figura 1 A). Con estas geometrías realistas evaluamos las propiedades térmicas efectivas y su relación con la microestructura. Las dos propiedades más relevantes fueron: dimensión fractal y relación volumen óseo/volumen total. Estos avances se presentaron en un congreso (Fajardo et al., 2018). En estos trabajos, en los que tuvieron participación de Fajardo, Ayala e Irastorza, apuntamos desarrollar los objetivos mencionados en la Introducción.

 

Figura 1.

Nota: Propiedades térmicas en tejido óseo trabecular bovino. (A) Corte de microtomografía. (B) Modelo en dos dimensiones de dos dominios: trabéculas (amarillo) y médula ósea (negro). (C) Simulación en 3D del mapa de temperatura utilizando el modelo realista.

 

También relacionado con el primer objetivo estamos escribiendo un texto de divulgación orientado a la resolución de problemas de multifísica con software libre, en el que comparamos diferentes protocolos de ablación en un tejido genérico. El trabajo es llevado adelante por Gómez (becario EVC CIN) e Irastorza y se utilizaron Gmsh (mallado), FEniCS (resolución de MEF), y Paraview y Matplotlib (visualización) (Gómez e Irastorza, 2020-2021, https://github.com/rirastorza/RFA-tutorial)

Por otro lado, también se desarrollaron simulaciones en modelos realistas antropomórficos en alta frecuencia para el estudio de otro problema: evaluación de salud ósea utilizando microondas. Si bien no fue parte del plan inicial de este proyecto, contribuyó al aprendizaje sobre la construcción de modelos antropomórficos a partir de imágenes médicas. El trabajo consistió en evaluar la sensibilidad en la detección del cambio de permitividad dieléctrica en una medición en el tobillo usando imágenes por microondas. Para eso se generaron modelos en dos dimensiones construidos a partir de imágenes de tomografía en tobillo (suministradas por el Centro de Diagnóstico Mon, La Plata). Con estos resultados publicamos un trabajo en una revista internacional (Fajardo et al., 2019).

 

Figura 2.

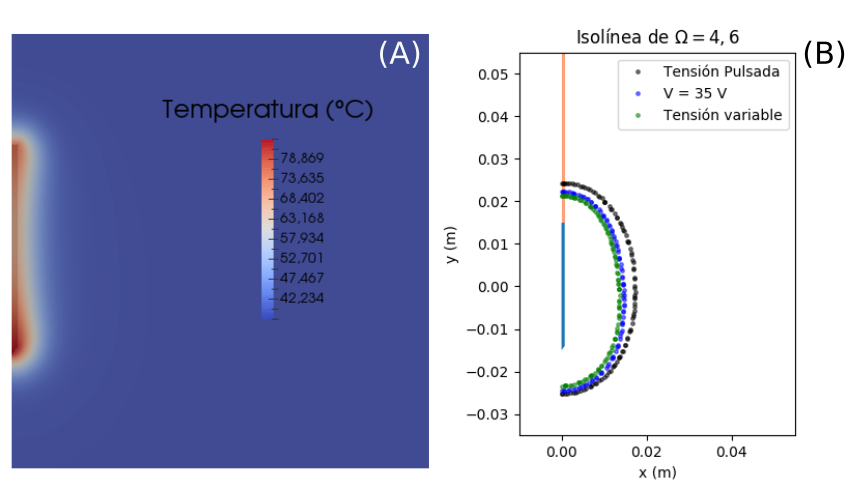Nota: Simulación de ARF en tejido genérico utilizando diferentes protocolos. (A) Mapa de temperatura al final de la simula- ción (aplicación de ARF durante 12 minutos) utilizando protocolo de tensión controlada (controlador Proporcional Integral) para cumplir con temperatura objetivo de 80 ℃. (B) Comparación de función de daño Ω (función de Arrhenius) de tres protocolos: tensión constante de 35 V, tensión pulsátil y tensión controlada.

 

En relación al objetivo (c) se simularon modelos realistas construidos a partir de tomografías computadas de torso completo. En particular, hemos interactuado con el doctor E. Berjano de la Universidad Politécnica de Valencia y doctora A. González Suárez de la Universidad Nacional de Galway, Irlanda (incorporada al proyecto en 2018). En estas investigaciones por medio de simulaciones cuantificamos la potencia absorbida en los diferentes tejidos en ablación para el tratamiento de arritmias por fibrilación auricular. Tenemos un trabajo en dos dimensiones enviado al congreso de la Sociedad Argentina de Bioingeniería 2020 (Irastorza, González Suárez et al., 2020) y otro publicado en revista internacional con un modelo en tres dimensiones (Irastorza, González-Suárez et al., 2020). En la Figura 3 se muestran las corrientes absorbidas por cada tejido en un corte tomográfico simulado.

Estamos trabajando con modelos antropomórficos de mallas completas obtenidas de Virtual Population (https://itis.swiss/virtual-population/virtual-population/overview/). En el escrito en preparación que estamos desarrollando con la doctora González Suárez estudiamos tratamientos de electroporación en corazón. También relacionado con el estudio de modelos realistas, comenzamos a estudiar la ARF del ganglio estrellado y obtuvimos resultados interesantes sobre la ubicación del electrodo, con lo cual generamos otro documento para publicar Irastorza et al., enviado para su publicación. En la Figura 4, se muestra la geometría de la simulación. El ganglio se encuentra en el cuello cercano a algunas arterias que complican su acceso, así como también su ablación.

Adicionalmente, como se mencionó se han explorado otros problemas vinculados con las propiedades dieléctricas y térmicas a escala molecular utilizando la técnica de dinámica molecular, lo que dio lugar a una publicación en revista internacional (Sánchez et al., 2019). Con esta técnica también se abordaron otros problemas relacionados con el comportamiento de un cristal de proteína (Howard et al., 2018; Espinosa et al., 2020), analizando su estabilidad y las condiciones más adecuadas para el estudio de estos sistemas cristalinos. Estas herramientas son útiles a la hora de estudiar, por ejemplo, un grupo de proteínas como lo son las fibras de colágeno, presentes en la mayoría de los tejidos.

Finalmente, en colaboración con Trujillo, González Suárez, Pérez y Berjano, se trabajó en un capítulo del libro “Principles and Technologies for Electromagnetic Energy Based Therapies” (Trujillo et al., 2021), que ha sido enviado para su corrección editorial.

 

Figura 3.

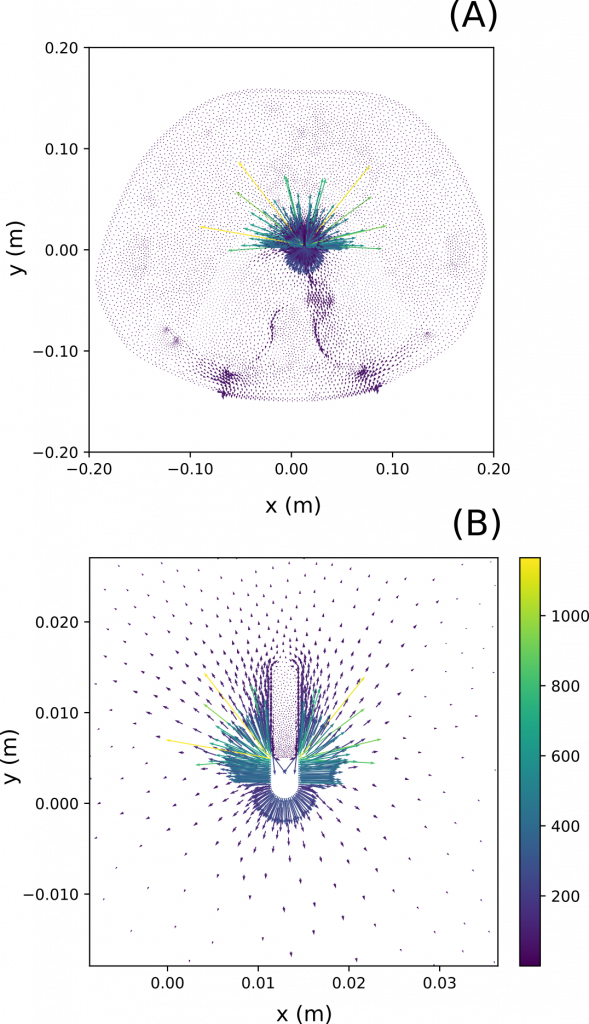
Nota: Densidad de corriente en modelo de torso completo. (A) Distribución de densidad de corriente (en A/m) en el tórax (modelo en 2D). (B) Detalle alrededor del electrodo activo.

 

Discusión

En líneas generales el proyecto ha cumplido con los objetivos particulares propuestos. Se han atacado diferentes problemáticas en la clínica tales como tratamiento de tumores, arritmias cardíacas, y recientemente ablación de ganglio estrellado. En los dos últimos casos se utilizaron además modelos antropomórficos realistas, lo cual requiere un alto costo computacional y, por lo tanto, la asignación inteligente de recursos. Remarcamos que como continuación de los proyectos anteriores también se modelaron experimentos que sirvieron para validación de los métodos numéricos implementados. Adicionalmente, se comenzó con una nueva línea relacionada con la simulación de modelos atomísticos utilizando dinámica molecular.

Un objetivo destacable de este proyecto es la formación de recursos humanos. En ese sentido, en el transcurso del proyecto hemos trabajado con dos becas EVC CIN: la de la ingeniera informática M. F. Ayala y la del estudiante de Bioingeniería Julián Gómez. Asimismo, se continuó con la formación del ahora doctor J. E. Fajardo (doctorado en marzo del 2020). También, en el transcurso del proyecto se dictaron dos cursos de posgrado en la UNAJ: “Herramientas de matemática aplicada” y “Métodos Estadísticos”.

Se han cumplido otros objetivos secundarios como; establecer vinculaciones con otros grupos de investigación nacionales e internacionales, y profesionales de la salud. Por ejemplo, con la mencionada doctora

1. González Suárez, quien se sumó al proyecto como colaboradora externa, además de la colaboración ya afianzada con el doctor E. Berjano. Además, mantenemos una fluida colaboración con la doctora G. Irastorza del Instituto Mon de diagnóstico por imágenes, quien nos provee de imágenes para la construcción de modelos realistas.

Finalmente, la implementación del software para el modelado con elementos finitos de problemas térmicos acoplados con los eléctricos íntegramente libre constituye un aspecto relevante del proyecto.

 

Figura 4.

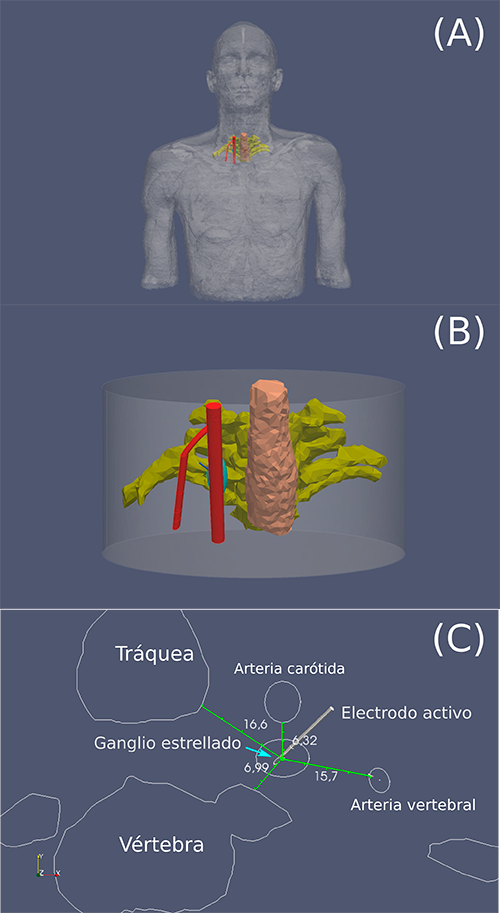
Nota: Modelo realista de cuello para simulación. (A) y (B) muestran la región en el cuello donde se encuentra el ganglio estrellado y las geometrías que se consideraron en la simulación. (C) Detalle de corte en dos dimensiones de las estructuras simuladas.

 

Conclusiones

En este proyecto se estableció un esquema de trabajo utilizando software libre y el método de elementos finitos para la resolución de problemas que involucran múltiples fenómenos físicos. Gran parte del código se encuentra accesible en un repositorio abierto que es de gran utilidad para la formación de recursos humanos. Adicionalmente, también se generaron rutinas para el procesamiento de imágenes médicas tanto para su caracterización como para la construcción de modelos antropomórficos para su posterior simulación. Se analizaron varias aplicaciones médicas, tales como, ablación cardíaca, ablación de tumores óseos y de ganglio estrellado. Como resultado de los desarrollos mencionados se publicaron varios artículos en revistas nacionales e internacionales, así como también publicaciones en congresos nacionales. Destacamos que durante el transcurso del proyecto se contribuyó al doctorado de un integrante y a la formación de una alumna (ahora ingeniera en informática) y un alumno estudiante de Bioingeniería.

 

Referencias bibliográficas

• Berjano, E. (2006). Theoretical modeling for radiofrequency ablation: state-of-the-art and challenges for the future. Biomedical engineering online, 5(1), 1-17.
• Brace, C. (2009). Radiofrequency and microwave ablation of the liver, lung, kidney, and bone: what are the differences? Current problems in diagnostic radiology, 38(3), 135-143.
• Espinosa, Y., Alvarez, H., Howard, E. y Carlevaro, C. (2020). Molecular dynamics simulation of the heart type fatty acid binding protein in a crystal environment. Journal of Biomolecular Structure and Dynamics, 1-10.
• Fajardo, E., Ayala, F., Carlevaro, C., F, V.e Irastorza, R. (2018). Microestructura y propiedades térmicas de hueso trabecular: mediciones y simulaciones computacionales. Reunión anual de física, Ciudad Autónoma de Buenos Aires, Argentina.
• Fajardo, J., Carlevaro, C., Vericat, F., Berjano, E. e Irastorza, R. (2018). Effect of the trabecular bone microstructure on measuring its thermal conductivity: a computer modeling-based study. Journal of thermal biology, 77, 131-136.
• Fajardo, J., Vericat, F., Irastorza, G., Carlevaro, C. e Irastorza, R. (2019). Sensitivity analysis on imaging the calcaneus using microwaves. Biomedical Physics & Engineering Express, 5(4), 045039.
• Gómez, J. e Irastorza, R. (2020-2021). Ablación por radiofrecuencia: estudios por simulación utilizando software libre. Manuscrito en preparación.
• Hasgall, P., Di Gennaro, F., Baumgartner, C., Neufeld, E., Gosselin, M., Payne, D., Klingenböck, A.y Kuster, N. (2015). IT’IS Database for thermal and electromagnetic parameters of biological tissues. Version 3.0. DOI: 10.13099/VIP21000-04-1. https://itis.swiss/virtual-population/tissue-properties/
• Howard, E., Cousido-Siah, A., Lepage, M., Schneider, J., Bodlenner, A., Mitschler, A., Meli, A., Izzo, I., Alva rez, H., Podjarny, A., et al. (2018). Structural Basis of Outstanding Multivalent Effects in Jack Bean α-Mannosidase Inhibition. Angewandte Chemie International Edition, 57 (27), 8002-8006.
• Irastorza, R., Bovaira, M., García-Vitoria, C., Muñoz, V.y Berjano, E. (enviado para su publicación). Pain Medicine.
• Irastorza, R., d’Avila, A. y Berjano, E. (2018). Thermal latency adds to lesion depth after application of high-power short-duration radiofrequency energy: Results of a computer-modeling study. Journal of cardiovascular electrophysiology, 29(2), 322-327.
• Irastorza, R., González Suárez, A. y Berjano, E. (2020). Analysis of electrical current distribution in the thorax during radiofrequency cardiac ablation: Preliminary results from a 2D computer model. Congreso Nacional de la Sociedad Argentina de Bioingeniería, Piriapolis, Uruguay.
• Irastorza, R., González-Suárez, A., Pérez, J.y Berjano, E. (2020). Differences in applied electrical power bet- ween full thorax models and limited-domain models for RF cardiac ablation. International Journal of Hyperthermia, 37 (1), 677-687.
• Irastorza, R., Trujillo, M.y Berjano, E. (2017). How coagulation zone size is underestimated in computer modeling of RF ablation by ignoring the cooling phase just after RF power is switched off. International journal for numerical methods in biomedical engineering, 33(11), 2869.
• Irastorza, R., Trujillo, M., Martel Villagrán, J.y Berjano, E. (2016). Computer modelling of RF ablation in cortical osteoid osteoma: assessment of the insulating effect of the reactive zone. International Journal of Hyperthermia, 32(3), 221-230.
• Kobza, R., Hindricks, G., Tanner, H., Schirdewahn, P., Dorszewski, A., Piorkowski, C., Gerds-Li, J.y Kottkamp, H. (2004). Late recurrent arrhythmias after ablation of atrial fibrillation: incidence, mechanisms, and treatment. Heart rhythm, 1(6), 676-683.
• Larson, M.y Bengzon, F. (2013). The finite element method: theory, implementation, and applications (Vol. 10). Springer Science & Business Media.
• Matschek, J., Bullinger, E., von Haeseler, F., Skalej, M. y Findeisen, R. (2017). Mathematical 3D modelling and sensitivity analysis of multipolar radiofrequency ablation in the spine. Mathematical biosciences, 284, 51-60.
• Rossmann, C. y Haemmerich, D. (2014). Review of temperature dependence of thermal properties, die- lectric properties, and perfusion of biological tissues at hyperthermic and ablation temperatures. Critical Reviews in Biomedical Engineering, 42(6).
• Sánchez, H., Irastorza, R. y Carlevaro, C. (2019). Uncertainties and temperature correction in molecular dynamic simulations of dielectric properties of condensed polar systems. Journal of Molecular Liquids, 278, 546-552.
• Trujillo, M., González-Suárez, A., Irastorza, R., Pérez, J. y Berjano, E. (2021). Radiofrequency Ablation. En P. Prakash y G. Srimathveeravalli (Eds.), Principles and Technologies for Electromagnetic Energy Based Therapies. Elsevier.
• Valvano, J., Cochran, J. y Diller, K. (1985). Thermal conductivity and diffusivity of biomaterials measured with self-heated thermistors. International Journal of Thermophysics, 6(3), 301-311.

 

Notas:

[1] rirastorza@unaj.edu.ar